Under construction.

 

 

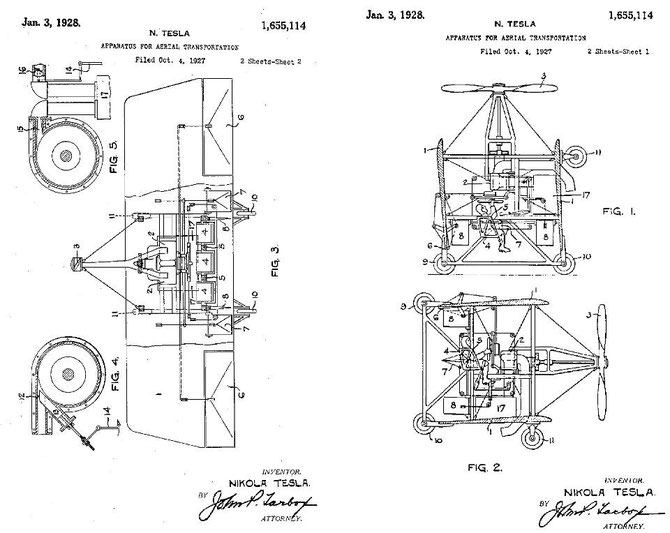
The latest inventions patented by Nikola Tesla are probablly the most mysterious because it seems that nobody still ever attempted to build and some of their principles and their purposes are also uknown.

 

In 1928 Tesla patented the invention for the "Apparatus for Aerial Transportation" that he claimed would revolutionise the world. This device would be powered by one of his miraculous turbines and would cost less than a thousand dollars.

 

• US1,655,113 -Method of Aerial Transportation- January 3, 1928

 

• US1,655,114 -Apparatus for Aerial Transportation- January 3, 1928

 

In those patents it is easy to appreciate that it had been designed by using many technical features of the conventional aviation and it could be compared to the ornithopter concept or the V-tol design, which could develop a vertical taking off like an helicopter and fly in horizontal position as an airplane when some altitude is achieved.

 

Today some of the most important aeronautic companies from around the world are searching for the right design which could make possible this method to avoid the risk which implies the common method of taking off and landing of the modern commertial aviation, knowing that most of the accidents usually doesn't happend during the flight but during the taking off and the landing.

 

 

The apparatus described in Tesla's patents seems to be quite simple but strange and it seems that he didn't have any intention to build any prototype. Another mistery is why Tesla patented an airplane like the patents US1,655,113 & US1,655,114 on January 3, 1928 when he'd already proposed the ultimate flying machine in 1919 and knowing that he wasn't very optimistic about the future of comertial aviation. One reason could be the difference of height. This awsome craft was to be powered by his World Wireless System, fly without wings or propellers, and would make war unthinkable by its ability to strike an enemy with impunity from thousands of miles away.

 

Maybe by the time Tesla conceded that airplanes might be useful after all, he was already behind the times. Four years before Tesla filed his own patent application, Albert Zahm, a versatile inventor with the Curtiss Aeroplane and Motor Corp.,  had come up with essentially the same idea.

 

 

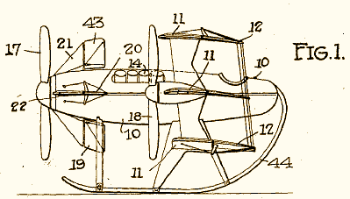
The airplane described in Zahm's patent US1,358,603 A - Hovering aeroplane - 9 Nov 1920 (Filed 10 Ago 1917) rocks backward on a set of skids (44), so that it can take off vertically like a helicopter. And where Tesla, who never designed a working aircraft, casually suggested that "the tail is omitted or, if used, it is retractable," Zahm's airplane adopts a canard configuration, with the "tail" located in front of the pilot. Zahm's pilot may may need to lie on his back during takeoff, but Tesla's solution, the swinging seat, hardly seems like an improvement.

 

According to Tesla's statements he was experimenting with his turbines with the objective of solving some of the problems of the existing airplanes of that times. And according to museum officials at The Nikola Tesla museum in Belgrade, he left sketches of interplanetary ships. This information, however is uknown.

 

Excerpt from “My Inventions” by Nikola Tesla, Chap. VI, last page:

“As stated on a previous occasion, when I was a student at college I conceived a flying machine quite unlike the present ones. The underlying principle was sound  but could not be carried into practice for want of a prime-mover of sufficiently great activity. In recent years I have successfully solved this problem and am now planning aerial machines devoid of sustaining planes, ailerons, propellers, and other external attachments which will be capable of immense speeds and are very likely to furnish powerful arguments for peace in the future. Such a machine, sustained and propelled entirely by reaction, is shown on page 108 and is supposed to be controlled either mechanically or by wireless energy.

 

By installing proper plants, it will be practicable to project a missile of this kind into the air and drop it almost on the very spot designated, which may be thousands of miles away."

 

In this ocasion Tesla stated that when he was an student he conceived a flying machine and "the underlying principle was sound". However, there are just few references in the articles describing the principles involved in this kind of "flying machine". Although it is unknown exactly how he was thinking to defy the law of gravity it is possible to levitate objects by sound.

 

Acoustic levitation is a method for suspending matter in a medium by using acoustic radiation pressure from intense sound waves in the medium.

Sometimes sound waves at ultrasonic frequencies can be used to levitate objects, thus creating no sound heard by the human ear, such as was demonstrated at Otsuka Lab,* while others use audible frequencies. There are various ways of emitting the sound wave, from creating a wave underneath the object and reflecting it back to its source, to using a (transparent) tank to create a large acoustic field.

Acoustic levitation is usually used for containerless processing which has become more important of late due to the small size and resistance of microchips and other such things in industry. Containerless processing may also be used for applications requiring very-high-purity materials or chemical reactions too rigorous to happen in a container. This method is harder to control than other methods of containerless processing such as electromagnetic levitation but has the advantage of being able to levitate nonconducting materials.

By 2013, acoustic levitation had progressed from motionless levitation to controllably moving hovering objects, an ability useful in the pharmaceutical and electronics industries.* A prototype device involved a chessboard-like array of square acoustic emitters that move an object from one square to another by slowly lowering the sound intensity emitted from one square while increasing the sound intensity from the other, allowing the object to travel virtually "downhill"

 

Current systems have lifted at most a few kilograms.* Acoustic levitators are used mostly in industry. However, some products are commercially available to the public.

 

 

 

Tesla's new self-propelled aerial tel-automaton. Devoid of propeller, sustaining wings and other means of external control. Could attain an speed of 350miles per hour (3600 m.p.h in another source), and will reach a determined point a thousand miles away accurately within a few feet.

 

---

 

Tesla explained that his "flying machine" would fly through the rarefied medium above the stratosphere at a height of 8 miles to reduce friction. With such conditions he stated that the velocity would be 3600 m.p.h.

 

Tesla Tells How We May Fly 8 Miles High At 1000 Miles An Hour - Reconstruction - July 1, 1919

 

It also would be able to remain absolutely stationary in the air. He described the engine as having 1000 horse power, and weighing only 100 lb. To make a comparison, one of the most powerfull turbine engine of the modern comertial aviation, a single GE90-115B puts out over 110,000 horsepower (the double of Titanic's engines), weihging 18.260 lb in empty condition.

 

Tesla Promises Big Things - New York Sun - September 12, 1911:

 

“How about aerial navigation?” Dr. Tesla was asked. He considered for a moment or two and then replied with great deliberation:

 

“The application of this principle will give the world a flying machine unlike anything that has ever been suggested before. It will have no planes, no screw propellers or devices of any kind hitherto used. It will be small and compact, excessively swift, and, above all, perfectly safe in the greatest storm. It can be built of any size and can carry any weight that may be desired”

 

 

Tesla's New Engine - New York Times - September 13, 1911

 

“Mr. Charles Wilson Price, editor of the Electrical Review, does not say that Nikola Tesla’s latest invention of a rotary engine operated by steam or gases will save most of the 30,000,000 horse power wasted annually by manufacturing plants in this country, power that is worth upward half a billion dollars. He has not said, as Mr. Tesla is reported saying, that the new engine will give the world a flying machine that, without planes or screw propellers, ‘excessively swift, and, above all, perfectly safe in the greatest storm, will be small and compact compared with present machines, but capable of carrying shiploads of passengers.”

 

 

The boy's book of new inventions - Maule, Harry E. (Harry Edward) - The Tesla Turbine” - 1912 - Pg. 268:

 

"I was a mechanical engineer before I was an electrical engineer, and besides, this principle was worked on in the course of my search for the ideal motor for airships, to be used in conjunction with my invention for the wireless transmission of electrical power. For twenty years I worked on the problem, but I have not given up. When my plan is perfected the present-day aeroplanes and dirigible balloons will disappear, and the dangerous sport of aviation, as we know it now with its hundreds of accidents, and its picturesque birdmen, will give way to safe, seaworthy airships, without wings or gas bags, but supported and driven by mechanical means".

 

“As I told you before when we were talking of the wireless transmission of power, the mechanism will be a development of the principle on which my turbine is constructed".

 

"It will be so tremendously powerful that it will make a veritable rope of air above the great machine to hold it at any altitude the navigators may choose, and also a rope of air in front or in the rear to send it forward or backward at almost any speed desired. When that day comes, airship travel will be as safe and prosaic as travel by railroad train today, and not much very different, except that there will be no dirt, and it will be much faster. One will be able to dine in New York, retire in an aero Pullman berth in a closed and perfectly furnished car, and arise to breakfast in London.”

 

 

Tesla's New Monarch of Machines - New York Herald - Oct. 15, 1911:

 

"With a thousand horse power engine, weighing only one hundred pounds, imagine the possibilities in automobiles, locomotives and steamships. In the space now occupied by the engines of the Lusitania twenty-five times her 80,000 horse power could be developed, were it possible to provide boiler capacity sufficient to furnish the necessary steam".

 

And it makes the aeroplane practical,— I suggested.

 

"Not the aeroplane, the flying machine,— responded Dr. Tesla. —Now you have struck the point in which I am most deeply interested—the object toward which I have been devoting my energies for more than twenty years—the dream of my life. It was in seeking the means of making the perfect flying machine that I developed this engine".

 

"The aeroplane is fatally defective. It is merely a toy—a sporting play-thing. It can never become commercially practical. It has fatal defects. One is the fact that when it encounters a downward current of air it is helpless. The —hole in the air— of which aviators speak is simply a downward current, and unless the aeroplane is high enough above the earth to move laterally but can do nothing but fall".

"The flying machine of the future—my flying machine—will be heavier than air, but it will not be an aeroplane. It will have no wings. It will be substantial, solid, stable. You cannot have a stable airplane. The gyroscope can never be successfully applied to the airplane, for it would give a stability that would result in the machine being torn to pieces by the wind, just as the unprotected aeroplane on the ground is torn to pieces by a high wind".

 

"You might see it on the ground and you would never guess that it was a flying machine. Yet it will be able to move at will through the air in any direction with perfect safety, higher speeds than have yet been reached, regardless of weather and oblivious of —holes in the air— or downward currents. It will ascend in such currents if desired. It can remain absolutely stationary in the air, even in a wind, for great length of time. Its lifting power will not depend upon any such delicate devices as the bird has to employ, but upon positive mechanical action".

 

You will get stability through gyroscopes? I asked.

 

"Through gyroscopic action of my engine, assisted by some devices I am not yet prepared to talk about", he replied.

 

"Powerful air currents that may be deflected at will, if produced by engines and compressors sufficiently light and powerful, might lift a heavy body off the ground and propel it through the air, I ventured, wondering if I had grasped the inventor's secret".

 

Dr. Tesla smiled an inscrutable smile.

 

"All I have to say on that point is that my airship will have neither gas bag, wings nor propellers, he said. It is the child of my dreams, the product of years of intense and painful toil and research. I am not going to talk about it any further. But whatever my airship may be, here at least is an engine that will do things that no other engine ever has done, and that is something tangible".

 

 

 

Tesla’s new device like bolts of Thor - New York Times - December 8, 1915:

 

"He is not yet ready to give the details of the engine which he says will render fruitless any military expedition against a country which possesses it. Suffice it to say that the destructive invention will go through space with a speed of 300miles per second, a manless airship without propelling engine or wings, sent by electricity to any desired point of the globe on its errand of destruction, if destruction its manipulator wishes to effect.”

 

 

Tesla Tells How We May Fly 8 Miles High At 1000 Miles An Hour - Reconstruction - July 1, 1919

 

"The idea is to fly at a great height where the air is rarefied, and therefore much less power is required to propel the machine through it".

 

"At a height of eight miles the decrease of oxygen can be overcome for both engine and aviator".

 

"The application of wireless power for aerial propulsion will do away with a great deal of complication and waste, and it is difficult to imagine that a more perfect means will ever be found to transport human beings to great distances economically. The power supply is virtually unlimited, as any number of power plants can be operated together, supplying energy to airships just as trains running on tracks are now supplied with electrical energy through rails or wires".

 

"In the future nations will fight each other thousands of miles apart. No soldier will see his enemy. In fact future wars will not be conducted by men directly but by the forces which if let loose may well destroy civilization completely. If war comes again, I look for the extensive use of self-propelled air vehicles carrying enormous charges of explosive which will be sent from any point to another to do their destructive work, with no human being aboard to guide them. The distance to which they can be sent is practically unlimited and the amount of explosive they can carry is likewise practically unlimited. It is practicable to send such an air vessel say to a distance of four or five thousand miles and so control its course either gyroscopically or electrically that it will land at the exact spot where it is intended to have it land, within a few feet, and its cargo of explosive can there be detonated. “This cannot be done by means of the present wireless plants, but with a proper plant it can be done"

 

 

Tesla, 75, Predicts New Power Source - New York Times - July 5th, 1931

 

"Mr. Tesla added he has devoted a great deal of time to experimentation with rocket-propelled ships and has designed a number of machines "with practical objects in view."

 

"A great development in this field may be confidently expected," he said. "With such machines it will be practicable to attain speeds of nearly a mile a second through the rarefied medium above the stratosphere.

 

"I anticipate that such machines will be of tremendous importance in international conflicts of the future. I foresee that in times not too distant wars between various countries will be carried on without a single combatant passing the border. At this very time it is possible to construct such infernal machines which will carry any desired quantity of poisoned gases and explosives, launch them against a target thousands of miles away and destroy a whole city".

 

 

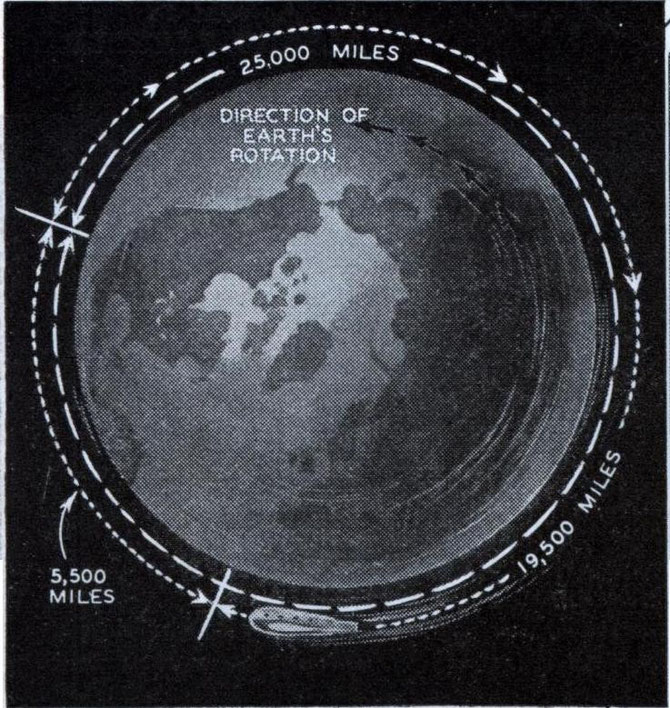
Radio Power will Revolutionize the World - Modern Mechanics - July, 1934

 

"Future rocket planes may circle the globe in 5 1/2 hours. At 3600 m.p.h the plane travels about 19,500 miles. Earth's rotation adds 5500 to the total".

 

 

 

In some occasion Tesla also suggested to use helium for de zeppelin designs instead of hydrogen which is inflammable and extremely explosive.

 

Can Radio Ignite Balloons? - by Nikola Tesla - Electrical Experimenter - October 1, 1919

 

"Why do the naval and other authorities allow such forms of aircraft to use an ex- plosive gas like hydrogen? A short time ago the press was filler? with the wondrous stories of how the U. S. Government experts had perfected the manufacture of the new! and non-inflammable balloon gas-helium, to such an extent that it was very cheap and readily obtainable in quantities. Funny, how these "new" inventions require so long a time to reach the public and those who need them. Helium, extracted from illuminating gas, is not new or wonderful at all".

 

Helium is an inert gas. Inert quite literally means non-combustible. In fact, helium in its liquid state is actually used as a coolant for things like rocket ships, MRI machines, and particle accelerators. Hindenburg blimp tragedy was filled with hydrogen, not helium.

 

 

 

• https://en.wikipedia.org/wiki/Acoustic_levitation